Issue 50 - Simulating Async Await

Simulating the behavior space of asynchronous await

Another weekend, another weekend read, this time all about simulating the behavior space of async await.

---

In this issue of The Weekend Read, we will simulate async await, more specifically, how an async await execution unfolds.

Simulating Executions

In Expression Evaluation and Fundamental Physics, Stephen Wolfram explores how expressions get evaluated:

This may all seem simple. But actually there are many surprisingly complicated and deep issues and questions. For example, to what extent can the evaluation events be applied in different orders, or in parallel? Does one always get the same answer? What about non-terminating sequences of events?

This fascinating blog post gave me the idea to explore how an async await execution unfolds via simulation.

Simulating Async Await

For the rest of this blog post, we will explore the calculation of Fibonacci numbers. Calculating Fibonacci is synchronous is nature, but we will implement two async variants simply for their illustrative advantages.

Quasi-Synchronous Calculation

The listing below shows a quasi-synchronous implementation of Fibonacci in Python-inspired pseudo code:

async def fib1(n):
  if n == 0 or n == 1:
    return 1
  else:
    p1 = async fib1(n-1)
    v1 = await p1
    p2 = async fib1(n-2)
    v2 = await p2
    return v1 + v2

Each recursive call is awaited after the invocation, ensuring the dependencies are resolved sequentially, that is, without any inherent non-determinism.

Asynchronous Calculation

The listing below shows an asynchronous implementation of Fibonacci in Python-inspired pseudo code:

async def fib2(n):
  if n == 0 or n == 1:
    return 1
  else:
    p1 = async fib1(n-1)
    p2 = async fib1(n-2)
    v1 = await p1
    v2 = await p2
    return v1 + v2

Both recursive calls are invoked first, and only then are their results awaited in order of the first and second call, allowing the dependencies to be resolved concurrently, that is, with inherent non-determinism.

Implementation

We will use Python to implement a minimal async await runtime on top of Python’s generators. A generator can either:

• yield an Invocation Command (I[func]) and subsequently be resumed with a reference to the resulting execution.

• yield an Await Command (A[exec]) and subsequently be resumed with the return value of the awaited execution

• terminate with a return value

# Represents an Invocation
class I:

    def __init__(self, func, args=[]):
        self.func = func
        self.args = args

# Represents a Suspension
class A:
    
    def __init__(self, exec):
        self.exec = exec

# Represents a Termination
class T:

    def __init__(self, resu):
        self.resu = resu

We wrap the Python generator into an Execution to track additional meta data we are interested in, most notably the previously yielded invoke commands, the yielded await commands, and if the execution is currently blocked on another execution.

class Execution:

    def __init__(self, uuid, coro):
        self._uuid = uuid
        self._coro = coro
        self._done = False
        self._resu = None
        self.invoked = []
        self.awaited = []
        self.blocked = None

    def next(self, value=None):
        try:
            if value is None:
                resul = next(self._coro)
            else:
                resul = self._coro.send(value)
            return resul
        except StopIteration as e:
            self._done = True
            self._resu = e.value
            return T(self._resu)
    
    def done(self):
        return self._done

This allows us to implement a simple scheduler that advances one step at a time until we receive a result.

class Scheduler:
    
 def __init__(self, random, init):
  self._universe = [init]
  self._runnable = [(init, None)]
  self._awaiting = []
  self._sequence = 0
  self._random = random

 def step(self):
  if not self._runnable:
   return
  
  # RANDOM SELECTION      
  (caller, value) = 
   self._runnable.pop(self._random.randint(0, len(self._runnable)-1))

  yielded = caller.next(value)

  if isinstance(yielded, I):
    callee = Execution(self._sequence, yielded.func(*yielded.args))
    self._universe.append(callee)
    self._runnable.append((callee, None))
    caller.invoked.append(callee)
    self._runnable.append((caller, callee))
    self._sequence += 1
 
  elif isinstance(yielded, A):
   caller.awaited.append(yielded.exec)
   if not yielded.exec.done():
    caller.blocked = yielded.exec
    self._awaiting.append(caller)
   else:
    self._runnable.append((caller, yielded.exec._resu))
 
  elif isinstance(yielded, T):
   self.callback(caller)

 def callback(self, recently_completed):
  unblocked = []
  for e in self._awaiting:
   if e.blocked == recently_completed:
    e.blocked = None
    self._runnable.append((e, recently_completed._resu))
    unblocked.append(e)
  self._awaiting = [t for t in self._awaiting if t not in unblocked]

Crucially, the scheduler is instantiate with a random number generator to randomly pick the next execution to advance.

Simulation

Running a 1000 simulations of quasi-synchronous or asynchronous calculation of Fibonacci is straight forward:

for seed in range(1000):

    s = Scheduler(random.Random(seed), Execution(0, fib1(3)))

    while s._runnable or s._awaiting:
        s.step()

By tracing the state of the scheduler, that is the state of all executions, and tracing the state transitions, we can build a transition graph of how the executions unfold.

Quasi-Synchronous Calculation

def fib1(n):
  if n == 0 or n == 1:
    return 1
  else:
    p1 = yield I(fib1, n-1)   
    v1 = yield A(p1)          
    p2 = yield I(fib1, n-2)
    v2 = yield A(p2)
    return v1 + v2

Here, the scheduler does not have a lot of choices: After fib1(3) yields the invoke command of fib1(2), the scheduler can either advance fib1(3) at which point fib1(3) blocks or it can advance fib1(2) which will itself face a similar choice, leading to a limited transition graph.

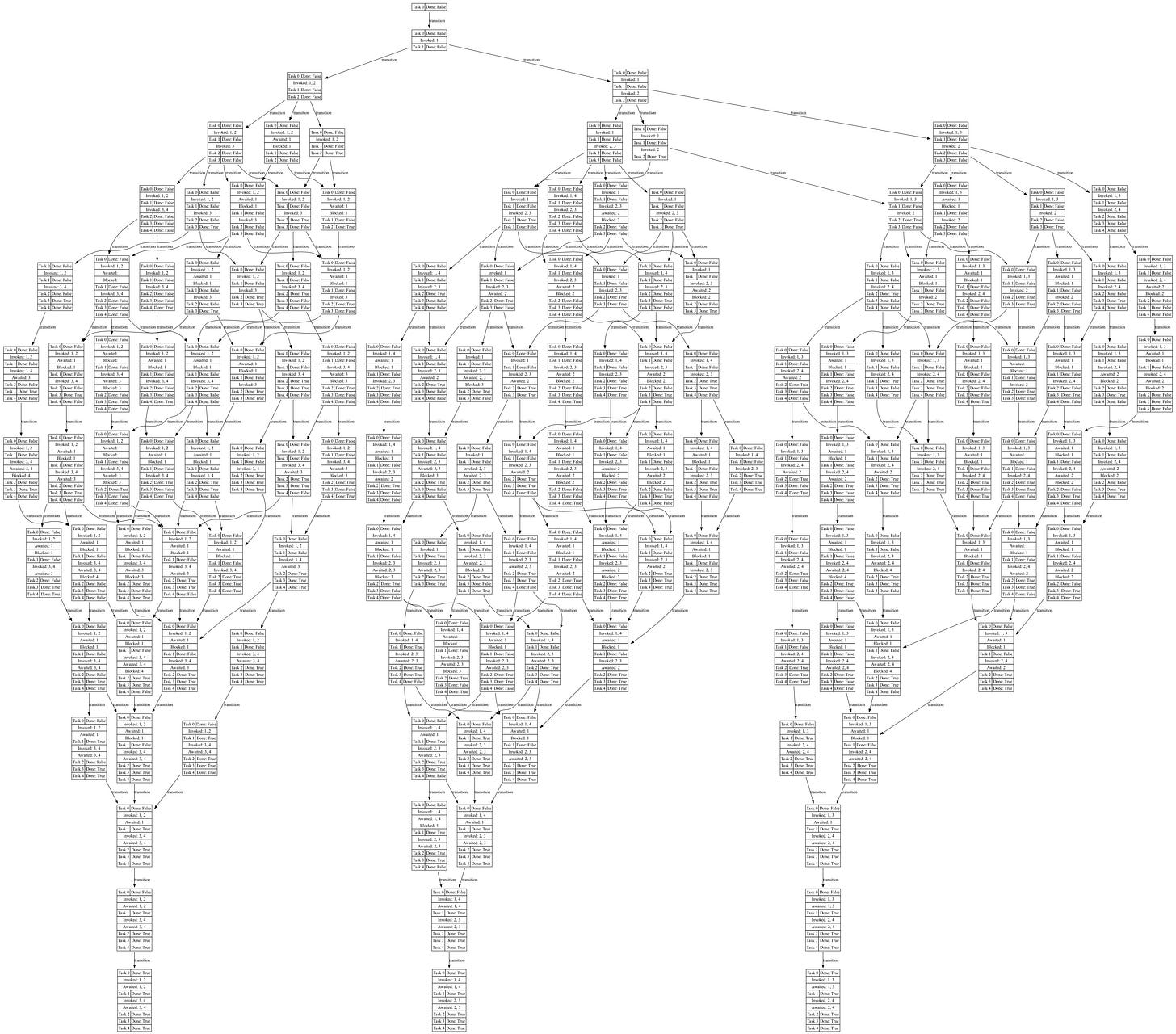
Asynchronous Calculation

def fib2(n):
  if n == 0 or n == 1:
    return 1
  else:
    p1 = yield I(fib1, n-1)       
    p2 = yield I(fib1, n-2)
    v1 = yield A(p1)    
    v2 = yield A(p2)
    return v1 + v2

Here, the scheduler has more choices: After fib2(3) yields the invoke command of fib2(2) and fib2(1), the scheduler can either advance fib2(3), fib2(2) or fib2(1), leading to a multitude of possibilities.

While this transition graph is much larger, we can still see echos of the first transition graph since we are still calculating the same function. Intuitively some resemblance is expected—although I did not have any expectation of how this resemblance may manifest itself a priori.

Conclusion

Simulation offers an intuitive lens into system behavior and allows us to quickly explore complex concepts and complex relationships, strengthening our understanding and inviting us to experiment.

Happy Reading